设(x)+(x)^2f(dfrac (1)(x))=dfrac ({x)^2+2x}(x+1) 求f(x)
设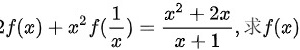
题目解答
答案
解:已知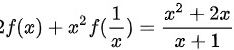
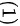 ,用
,用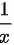 替换(1)式中的
替换(1)式中的 可得,
可得,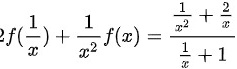 ,整理可得,
,整理可得,
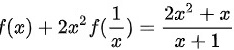 (2)
(2)
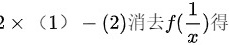
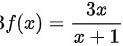 ,所以,
,所以,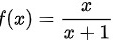
解析
考查要点:本题主要考查函数方程的解法,特别是通过变量替换构造方程组并消元的方法。
解题核心思路:
- 变量替换:将原方程中的$x$替换为$\dfrac{1}{x}$,得到第二个方程。
- 联立方程组:通过联立原方程和替换后的方程,消去$f\left(\dfrac{1}{x}\right)$,解出$f(x)$。
- 代数运算:注意分式化简和方程的线性组合,确保运算过程中符号和系数的准确性。
破题关键点:
- 正确替换变量,确保替换后的方程与原方程形式一致。
- 合理选择方程组合方式,通过乘法调整系数,实现消元目标。
原方程:
$2f(x) + x^{2}f\left(\dfrac{1}{x}\right) = \dfrac{x^{2} + 2x}{x + 1} \quad \text{(1)}$
步骤1:变量替换
将$x$替换为$\dfrac{1}{x}$,得到:
$2f\left(\dfrac{1}{x}\right) + \dfrac{1}{x^{2}}f(x) = \dfrac{\dfrac{1}{x^{2}} + \dfrac{2}{x}}{\dfrac{1}{x} + 1} \quad \text{(2)}$
步骤2:化简方程(2)
分子:$\dfrac{1}{x^{2}} + \dfrac{2}{x} = \dfrac{1 + 2x}{x^{2}}$
分母:$\dfrac{1}{x} + 1 = \dfrac{1 + x}{x}$
因此,方程(2)化简为:
$2f\left(\dfrac{1}{x}\right) + \dfrac{1}{x^{2}}f(x) = \dfrac{1 + 2x}{x(x + 1)}$
步骤3:调整方程形式
将方程(2)两边乘以$x^{2}$,得到:
$2x^{2}f\left(\dfrac{1}{x}\right) + f(x) = \dfrac{x(1 + 2x)}{x + 1} \quad \text{(2a)}$
步骤4:联立方程消元
- 方程(1):$2f(x) + x^{2}f\left(\dfrac{1}{x}\right) = \dfrac{x^{2} + 2x}{x + 1}$
- 方程(2a):$f(x) + 2x^{2}f\left(\dfrac{1}{x}\right) = \dfrac{x(1 + 2x)}{x + 1}$
操作:将方程(1)乘以2,再减去方程(2a):
$\begin{aligned}4f(x) + 2x^{2}f\left(\dfrac{1}{x}\right) & = \dfrac{2(x^{2} + 2x)}{x + 1} \\\underline{-\quad f(x) - 2x^{2}f\left(\dfrac{1}{x}\right)} & \underline{= -\dfrac{x(1 + 2x)}{x + 1}} \\3f(x) & = \dfrac{3x}{x + 1}\end{aligned}$
步骤5:解得$f(x)$
$f(x) = \dfrac{x}{x + 1}$