题目
4)求微分方程 +(xy+x-(e)^y)dy=0 的通解.
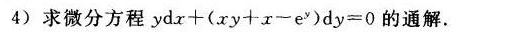
题目解答
答案
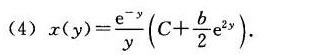
解析
步骤 1:确定方程类型
给定的微分方程是 $ydx+(xy+x-{e}^{y})dy=0$。这是一个一阶线性微分方程,因为它可以写成 $M(x,y)dx+N(x,y)dy=0$ 的形式,其中 $M(x,y)=y$ 和 $N(x,y)=xy+x-{e}^{y}$。
步骤 2:检查是否为全微分方程
为了确定是否为全微分方程,我们需要检查 $\frac{\partial M}{\partial y}$ 是否等于 $\frac{\partial N}{\partial x}$。计算得 $\frac{\partial M}{\partial y}=1$ 和 $\frac{\partial N}{\partial x}=y+1$。由于 $\frac{\partial M}{\partial y} \neq \frac{\partial N}{\partial x}$,所以这不是一个全微分方程。
步骤 3:寻找积分因子
由于方程不是全微分方程,我们需要寻找一个积分因子 $\mu(x,y)$,使得 $\mu(x,y)M(x,y)dx+\mu(x,y)N(x,y)dy=0$ 成为全微分方程。我们尝试寻找只依赖于 $y$ 的积分因子,即 $\mu(y)$。根据积分因子的条件,我们有 $\frac{1}{\mu(y)}\frac{d\mu(y)}{dy}=\frac{\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}}{M(x,y)}$。代入 $M(x,y)$ 和 $N(x,y)$ 的值,得到 $\frac{1}{\mu(y)}\frac{d\mu(y)}{dy}=\frac{y+1-1}{y}=\frac{y}{y}=1$。解这个方程得到 $\mu(y)={e}^{y}$。
步骤 4:应用积分因子
将积分因子 $\mu(y)={e}^{y}$ 乘以原方程,得到 ${e}^{y}ydx+({e}^{y}xy+{e}^{y}x-{e}^{2y})dy=0$。现在,我们检查是否为全微分方程。计算 $\frac{\partial ({e}^{y}y)}{\partial y}={e}^{y}y+{e}^{y}$ 和 $\frac{\partial ({e}^{y}xy+{e}^{y}x-{e}^{2y})}{\partial x}={e}^{y}y+{e}^{y}$。由于 $\frac{\partial ({e}^{y}y)}{\partial y}=\frac{\partial ({e}^{y}xy+{e}^{y}x-{e}^{2y})}{\partial x}$,所以这是一个全微分方程。
步骤 5:求解全微分方程
由于这是一个全微分方程,我们可以通过积分找到通解。积分 ${e}^{y}ydx+({e}^{y}xy+{e}^{y}x-{e}^{2y})dy=0$,得到 $\int {e}^{y}ydx+\int ({e}^{y}xy+{e}^{y}x-{e}^{2y})dy=C$。由于 $dx$ 和 $dy$ 是独立的,我们可以分别积分。对于 $x$ 的部分,我们有 $\int {e}^{y}ydx=y{e}^{y}x$。对于 $y$ 的部分,我们有 $\int ({e}^{y}xy+{e}^{y}x-{e}^{2y})dy=\frac{1}{2}{e}^{2y}x-{e}^{2y}+C$。因此,通解为 $y{e}^{y}x+\frac{1}{2}{e}^{2y}x-{e}^{2y}=C$。整理得到 $x(y)=\dfrac {{e}^{-y}}{y}(C+\dfrac {1}{2}{e}^{2y})$。
给定的微分方程是 $ydx+(xy+x-{e}^{y})dy=0$。这是一个一阶线性微分方程,因为它可以写成 $M(x,y)dx+N(x,y)dy=0$ 的形式,其中 $M(x,y)=y$ 和 $N(x,y)=xy+x-{e}^{y}$。
步骤 2:检查是否为全微分方程
为了确定是否为全微分方程,我们需要检查 $\frac{\partial M}{\partial y}$ 是否等于 $\frac{\partial N}{\partial x}$。计算得 $\frac{\partial M}{\partial y}=1$ 和 $\frac{\partial N}{\partial x}=y+1$。由于 $\frac{\partial M}{\partial y} \neq \frac{\partial N}{\partial x}$,所以这不是一个全微分方程。
步骤 3:寻找积分因子
由于方程不是全微分方程,我们需要寻找一个积分因子 $\mu(x,y)$,使得 $\mu(x,y)M(x,y)dx+\mu(x,y)N(x,y)dy=0$ 成为全微分方程。我们尝试寻找只依赖于 $y$ 的积分因子,即 $\mu(y)$。根据积分因子的条件,我们有 $\frac{1}{\mu(y)}\frac{d\mu(y)}{dy}=\frac{\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}}{M(x,y)}$。代入 $M(x,y)$ 和 $N(x,y)$ 的值,得到 $\frac{1}{\mu(y)}\frac{d\mu(y)}{dy}=\frac{y+1-1}{y}=\frac{y}{y}=1$。解这个方程得到 $\mu(y)={e}^{y}$。
步骤 4:应用积分因子
将积分因子 $\mu(y)={e}^{y}$ 乘以原方程,得到 ${e}^{y}ydx+({e}^{y}xy+{e}^{y}x-{e}^{2y})dy=0$。现在,我们检查是否为全微分方程。计算 $\frac{\partial ({e}^{y}y)}{\partial y}={e}^{y}y+{e}^{y}$ 和 $\frac{\partial ({e}^{y}xy+{e}^{y}x-{e}^{2y})}{\partial x}={e}^{y}y+{e}^{y}$。由于 $\frac{\partial ({e}^{y}y)}{\partial y}=\frac{\partial ({e}^{y}xy+{e}^{y}x-{e}^{2y})}{\partial x}$,所以这是一个全微分方程。
步骤 5:求解全微分方程
由于这是一个全微分方程,我们可以通过积分找到通解。积分 ${e}^{y}ydx+({e}^{y}xy+{e}^{y}x-{e}^{2y})dy=0$,得到 $\int {e}^{y}ydx+\int ({e}^{y}xy+{e}^{y}x-{e}^{2y})dy=C$。由于 $dx$ 和 $dy$ 是独立的,我们可以分别积分。对于 $x$ 的部分,我们有 $\int {e}^{y}ydx=y{e}^{y}x$。对于 $y$ 的部分,我们有 $\int ({e}^{y}xy+{e}^{y}x-{e}^{2y})dy=\frac{1}{2}{e}^{2y}x-{e}^{2y}+C$。因此,通解为 $y{e}^{y}x+\frac{1}{2}{e}^{2y}x-{e}^{2y}=C$。整理得到 $x(y)=\dfrac {{e}^{-y}}{y}(C+\dfrac {1}{2}{e}^{2y})$。