题目
1.求下列极限:-|||-(12) lim _(xarrow 0)(x)^2(e)^dfrac (1{{x)^2}} ;
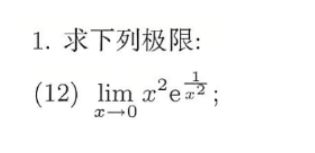
题目解答
答案
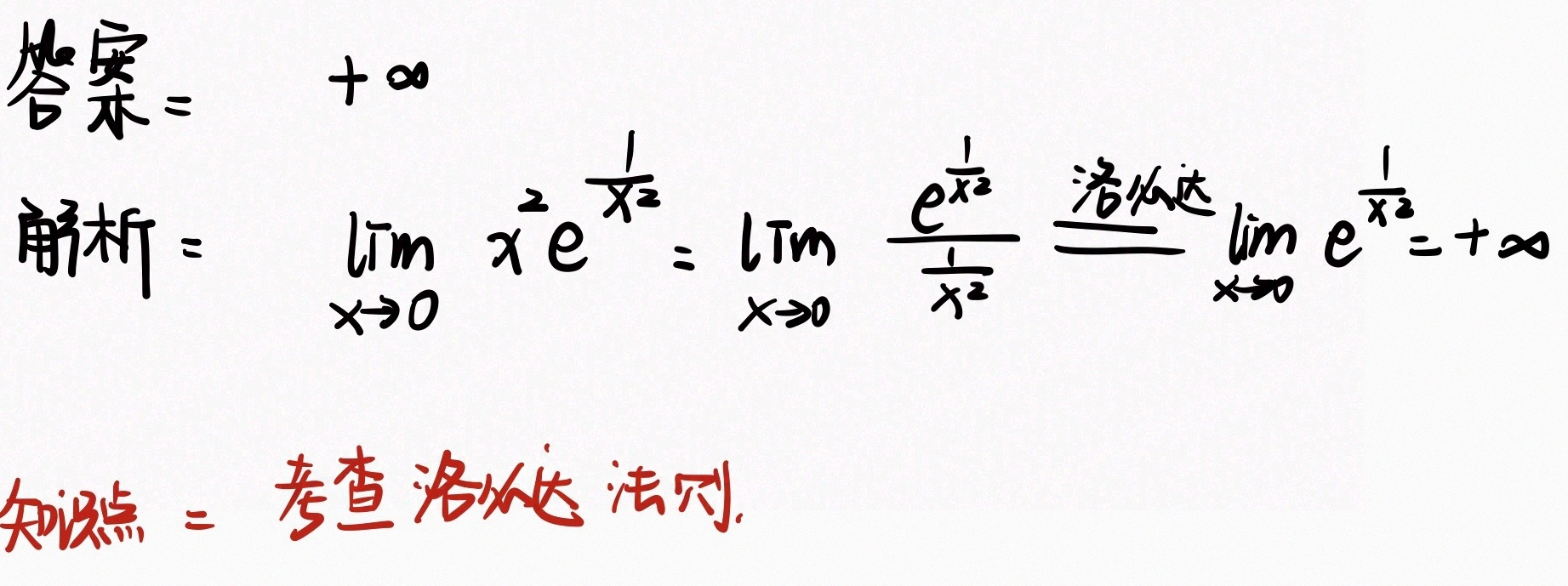
解析
题目1:求极限$\lim _{x\rightarrow 0}{x}^{2}{e}^{\frac{1}{{x}^{2}}}$
考察知识:极限计算(含指数函数的极限)、变量替换法。
解题思路:
当$x\rightarrow0$时,$\frac{1}{x^2}\rightarrow+\infty$,指数函数$e^{\frac{1}{x^2}}$趋向于$+\infty$,但$x^2$趋向于$0$,属于“$0\cdot\infty$型”极限,需转化为分式形式用洛必达法则或变量替换。
方法一:变量替换
设$t=\frac{1}{x^2}$,则当$x\rightarrow0$时,$t\rightarrow+\infty$,且$x^2=\fracfrac{1}{t}$,原式转化为:
$\lim _{x\rightarrow 0}{x}^{2}{e}^{\frac{1}{{x}^{2}}}=\lim _{t\rightarrow+\infty}\frac{e^t}{t}$
此为“$\frac{\infty}{\infty}$型”极限,适用洛必达法则:
- 分子导数:$(e^t)'=e^t$
- 分母导数:$t'=1$
多次求导后仍为$\frac{e^t}{1}\rightarrow+\infty$,故极限为$+\infty$。