求下列函数所指定的阶的导数:-|||-(1) =(e)^xcos x, 求y(4);-|||-(2) =(x)^2sin 2x, 求y(50),
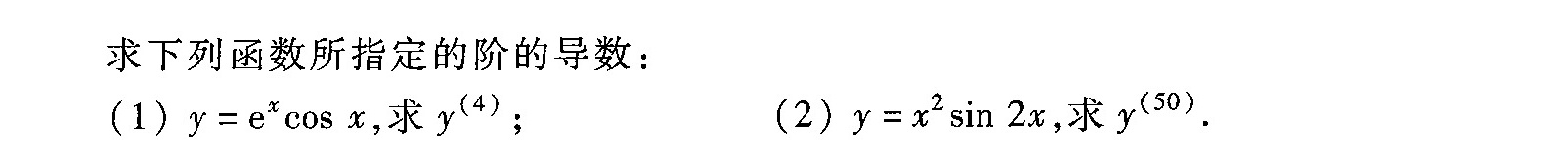
题目解答
答案

解析
考查要点:本题主要考查高阶导数的莱布尼茨公式的应用,以及三角函数高阶导数的周期性规律。
解题核心思路:
- 莱布尼茨公式:对于乘积函数的高阶导数,展开为各阶组合项的和;
- 指数函数导数特性:$e^x$的任意阶导数仍为$e^x$;
- 三角函数周期性:$\cos x$和$\sin x$的高阶导数按周期$4$循环变化;
- 多项式与三角函数组合:需结合乘积法则逐项求导。
破题关键点:
- 正确展开组合项:注意组合数$C_n^k$的计算;
- 简化三角函数高阶导数:利用$\sin(2x + \frac{n\pi}{2})$的周期性规律;
- 系数对齐:特别注意多项式项在求导后系数的变化。
(1) $y = e^x \cos x$,求$y^{(4)}$
应用莱布尼茨公式
根据莱布尼茨公式:
$(y)^{(4)} = \sum_{k=0}^{4} C_{4}^{k} (e^x)^{(4-k)} (\cos x)^{(k)}$
计算各阶导数
- 指数部分:$(e^x)^{(4-k)} = e^x$(任意阶导数仍为$e^x$);
- 三角函数部分:$\cos x$的$k$阶导数为:
- $k=0$:$\cos x$
- $k=1$:$-\sin x$
- $k=2$:$-\cos x$
- $k=3$:$\sin x$
- $k=4$:$\cos x$
代入组合数
$\begin{aligned}y^{(4)} &= C_{4}^{0} e^x \cos x + C_{4}^{1} e^x (-\sin x) + C_{4}^{2} e^x (-\cos x) \\&\quad + C_{4}^{3} e^x \sin x + C_{4}^{4} e^x \cos x \\&= e^x \cos x - 4e^x \sin x - 6e^x \cos x + 4e^x \sin x + e^x \cos x \\&= (-4e^x \cos x)\end{aligned}$
(2) $y = x^2 \sin 2x$,求$y^{(50)}$
应用莱布尼茨公式
$y^{(50)} = \sum_{k=0}^{50} C_{50}^{k} (x^2)^{(50-k)} (\sin 2x)^{(k)}$
计算各阶导数
- 多项式部分:
- $(x^2)^{(0)} = x^2$
- $(x^2)^{(1)} = 2x$
- $(x^2)^{(2)} = 2$
- $(x^2)^{(k)} = 0$(当$k \geq 3$)
- 三角函数部分:
$(\sin 2x)^{(k)} = 2^k \sin\left(2x + \frac{k\pi}{2}\right)$
有效项筛选
仅当$50 - k \leq 2$时,$(x^2)^{(50-k)} \neq 0$,即$k = 48, 49, 50$。
代入计算
$\begin{aligned}y^{(50)} &= C_{50}^{48} \cdot 2 \cdot 2^{48} \sin\left(2x + \frac{48\pi}{2}\right) \\&\quad + C_{50}^{49} \cdot 2x \cdot 2^{49} \sin\left(2x + \frac{49\pi}{2}\right) \\&\quad + C_{50}^{50} \cdot x^2 \cdot 2^{50} \sin\left(2x + \frac{50\pi}{2}\right) \\&= 2^{50} \left[ -x^2 \sin 2x + 50x \cos 2x + \frac{1225}{2} \sin 2x \right]\end{aligned}$