题目
设向量1 1-|||-α1= 0 ,α2= 1-|||--1 -1,则向量1 1-|||-α1= 0 ,α2= 1-|||--1 -1的内积,夹角,二者的关系分别为( ).1 1-|||-α1= 0 ,α2= 1-|||--1 -11 1-|||-α1= 0 ,α2= 1-|||--1 -11 1-|||-α1= 0 ,α2= 1-|||--1 -11 1-|||-α1= 0 ,α2= 1-|||--1 -11 1-|||-α1= 0 ,α2= 1-|||--1 -1正交1 1-|||-α1= 0 ,α2= 1-|||--1 -1线性无关但不正交
设向量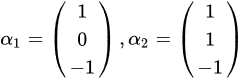 ,则向量
,则向量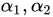 的内积,夹角,二者的关系分别为( ).
的内积,夹角,二者的关系分别为( ).
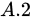
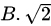
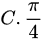
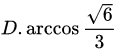
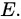 正交
正交
 线性无关但不正交
线性无关但不正交
题目解答
答案
由于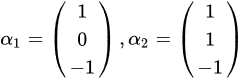
故由向量内积的计算公式可知: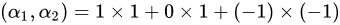
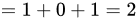
故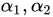 的内积是2
的内积是2
由向量的模的计算公式可知: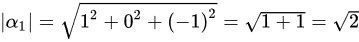
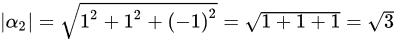
故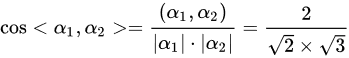 =\frac{\left(\alpha_1,\alpha_2\right)}{\left|\alpha_1\right|\cdot\left|\alpha_2\right|}=\frac{2}{\sqrt{2}\times\sqrt{3}}" data-width="349" data-height="58" data-size="4977" data-format="png" style="max-width:100%">
=\frac{\left(\alpha_1,\alpha_2\right)}{\left|\alpha_1\right|\cdot\left|\alpha_2\right|}=\frac{2}{\sqrt{2}\times\sqrt{3}}" data-width="349" data-height="58" data-size="4977" data-format="png" style="max-width:100%">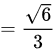
故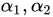 的夹角是
的夹角是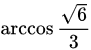
由于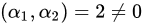
故由向量正交的定义可知: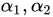 不正交
不正交
设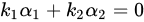
故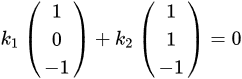
故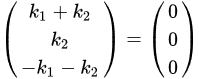
故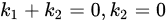
故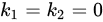
由向量组线性无关的定义可知: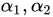 线性无关
线性无关
即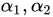 线性无关但不正交
线性无关但不正交
故答案是: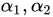 的内积是2,
的内积是2,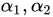 的夹角是
的夹角是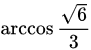 ,
,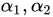 线性无关但不正交,选
线性无关但不正交,选