题目
函数(z)=(x)^2+(y)^2i ( ).A.仅在(z)=(x)^2+(y)^2i上解析;B.在除(z)=(x)^2+(y)^2i之外的复平面上解析;C.在(z)=(x)^2+(y)^2i上可导,但在复平面上处处不解析;D.在整个复平面上解析.
函数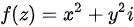 ( ).
( ).
A.仅在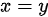 上解析;
上解析;
B.在除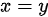 之外的复平面上解析;
之外的复平面上解析;
C.在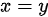 上可导,但在复平面上处处不解析;
上可导,但在复平面上处处不解析;
D.在整个复平面上解析.
题目解答
答案
本题考查复变函数.
由题意,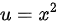 ,
,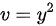 .
.
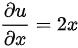 ,
,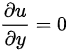 .
.
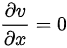 ,
,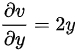 .
.
当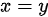 时,才会满足柯西黎曼方程,即:
时,才会满足柯西黎曼方程,即:
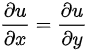 ,
,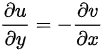 .
.
故函数仅在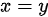 上解析.
上解析.
因此本题答案选A,排除B,C,D.
解析
本题考查复变函数的解析性判断,核心在于柯西-黎曼方程的应用。函数$f(z)=x^2 + y^2i$的实部$u=x^2$,虚部$v=y^2$。需计算偏导数,验证柯西-黎曼方程$\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}$和$\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}$是否成立,并分析解的区域。
关键点:
- 柯西-黎曼方程是判断复变函数解析性的必要条件;
- 解析性要求函数在某点的邻域内满足柯西-黎曼方程,而不仅仅是单个点。
-
分解函数
$f(z) = u(x,y) + iv(x,y)$,其中$u = x^2$,$v = y^2$。 -
计算偏导数
- $\frac{\partial u}{\partial x} = 2x$,$\frac{\partial u}{\partial y} = 0$
- $\frac{\partial v}{\partial x} = 0$,$\frac{\partial v}{\partial y} = 2y$
-
代入柯西-黎曼方程
- $\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \Rightarrow 2x = 2y \Rightarrow x = y$
- $\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x} \Rightarrow 0 = 0$(恒成立)
-
分析解的区域
- 柯西-黎曼方程仅在直线$x=y$上成立,但该直线是零测集,不存在包含这些点的邻域,因此函数在复平面上处处不解析,仅在$x=y$上可导。