题目
求下列函数的极值点:___-|||-=3axy-(x)^3-(y)^3(agt 0);
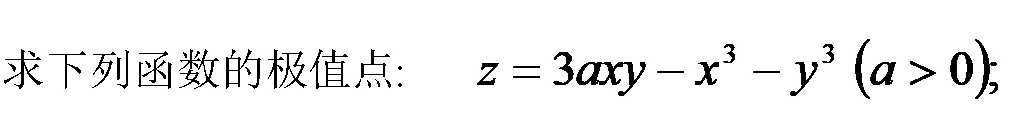
题目解答
答案
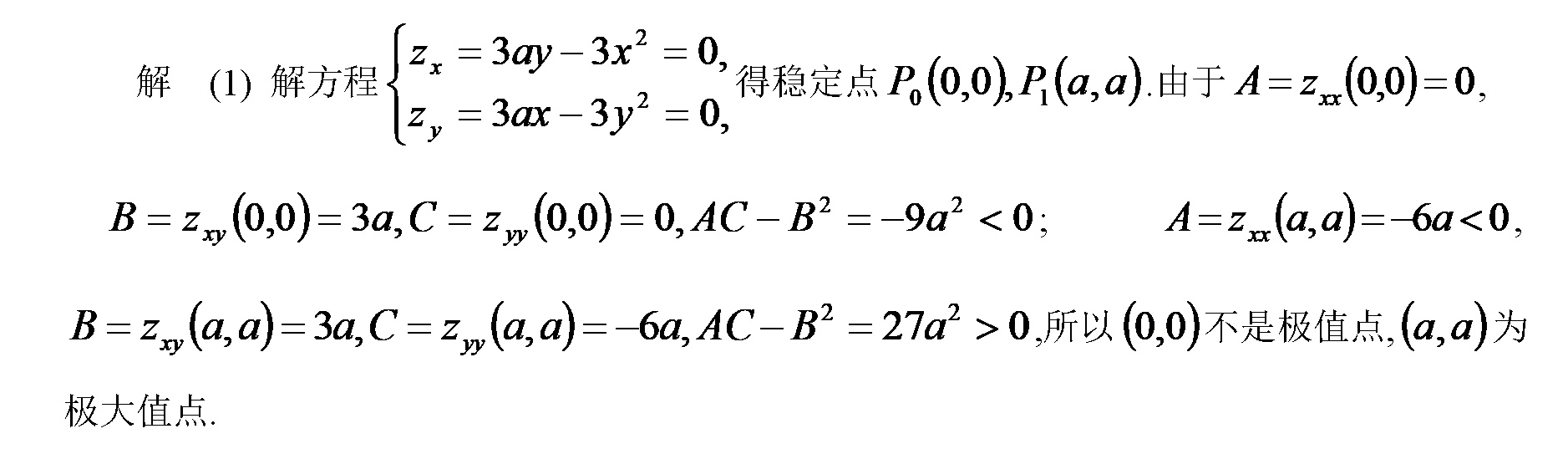
解析
考查要点:本题主要考查二元函数极值点的求解方法,包括一阶偏导数求解临界点和二阶导数检验法的应用。
解题核心思路:
- 求一阶偏导数,联立方程组解出临界点;
- 计算二阶偏导数,构造Hessian矩阵;
- 判断Hessian行列式 $AC - B^2$ 的符号,结合 $A$ 的符号确定临界点的性质。
破题关键点:
- 正确求解偏导数,特别注意混合偏导数的计算;
- 代入临界点时,准确计算二阶偏导数的值;
- Hessian行列式的符号决定临界点是否为极值点,结合 $A$ 的符号进一步判断极大或极小。
步骤1:求一阶偏导数并解方程组
函数 $z = 3axy - x^3 - y^3$ 的一阶偏导数为:
$\begin{cases}z_x = 3ay - 3x^2 = 0 \\z_y = 3ax - 3y^2 = 0\end{cases}$
解方程组:
- 情况1:$x = 0$,代入第二个方程得 $y = 0$,临界点为 $(0, 0)$;
- 情况2:联立 $3ay = 3x^2$ 和 $3ax = 3y^2$,消去系数得:
$y = \frac{x^2}{a}, \quad x = \frac{y^2}{a}$
代入消元得 $x = a$,对应 $y = a$,临界点为 $(a, a)$。
步骤2:计算二阶偏导数
$\begin{cases}z_{xx} = -6x \\z_{xy} = 3a \\z_{yy} = -6y\end{cases}$
步骤3:二阶导数检验法
-
点 $(0, 0)$:
- $A = z_{xx}(0,0) = 0$,$B = z_{xy}(0,0) = 3a$,$C = z_{yy}(0,0) = 0$;
- Hessian行列式 $AC - B^2 = 0 \cdot 0 - (3a)^2 = -9a^2 < 0$,不是极值点。
-
点 $(a, a)$:
- $A = z_{xx}(a,a) = -6a$,$B = z_{xy}(a,a) = 3a$,$C = z_{yy}(a,a) = -6a$;
- Hessian行列式 $AC - B^2 = (-6a)(-6a) - (3a)^2 = 27a^2 > 0$,且 $A < 0$,为极大值点。