题目
设 y=y(x) 是由 sin (xy)=ln dfrac (x+e)(y)+1 确定的隐函数,求y`(0)和 y``(0)的值.

题目解答
答案
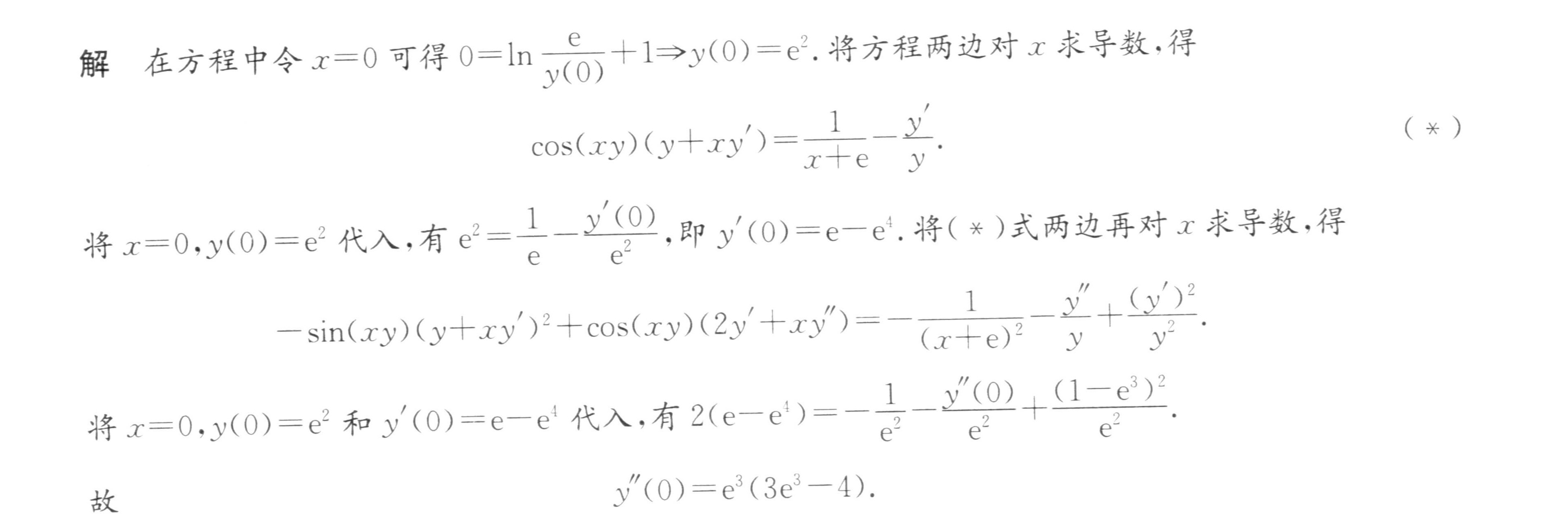
解析
步骤 1:确定 y(0) 的值
在方程 $\sin (xy)=\ln \dfrac {x+e}{y}+1$ 中令 x=0,得到 $\sin (0)=\ln \dfrac {e}{y}+1$,即 $0=\ln \dfrac {e}{y}+1$。解得 $y(0)={e}^{2}$。
步骤 2:求导数 y'(x)
将方程两边对x求导,得到 $\cos (xy)(y+xy')=\dfrac {1}{x+e}-\dfrac {y'}{y}$。将 x=0 和 $y(0)={e}^{2}$ 代入,得到 ${e}^{2}=\dfrac {1}{e}-\dfrac {y'(0)}{{e}^{2}}$。解得 $y'(0)={e}^{-{e}^{4}}$。
步骤 3:求导数 y''(x)
将上一步得到的导数方程两边再对x求导,得到 $-\sin (xy)(y+xy')^2+\cos (xy)(y'+xy'')=\dfrac {-1}{{(x+e)}^{2}}-\dfrac {y''}{y}+\dfrac {(y')^2}{y^2}$。将 x=0,$y(0)={e}^{2}$,$y'(0)={e}^{-{e}^{4}}$ 代入,得到 $2(e-{e}^{4})=-\dfrac {1}{{e}^{2}}-\dfrac {y''(0)}{{e}^{2}}+\dfrac {{(1-{e}^{3})}^{2}}{{e}^{2}}$。解得 $y''(0)={e}^{3}(3{e}^{3}-4)$。
在方程 $\sin (xy)=\ln \dfrac {x+e}{y}+1$ 中令 x=0,得到 $\sin (0)=\ln \dfrac {e}{y}+1$,即 $0=\ln \dfrac {e}{y}+1$。解得 $y(0)={e}^{2}$。
步骤 2:求导数 y'(x)
将方程两边对x求导,得到 $\cos (xy)(y+xy')=\dfrac {1}{x+e}-\dfrac {y'}{y}$。将 x=0 和 $y(0)={e}^{2}$ 代入,得到 ${e}^{2}=\dfrac {1}{e}-\dfrac {y'(0)}{{e}^{2}}$。解得 $y'(0)={e}^{-{e}^{4}}$。
步骤 3:求导数 y''(x)
将上一步得到的导数方程两边再对x求导,得到 $-\sin (xy)(y+xy')^2+\cos (xy)(y'+xy'')=\dfrac {-1}{{(x+e)}^{2}}-\dfrac {y''}{y}+\dfrac {(y')^2}{y^2}$。将 x=0,$y(0)={e}^{2}$,$y'(0)={e}^{-{e}^{4}}$ 代入,得到 $2(e-{e}^{4})=-\dfrac {1}{{e}^{2}}-\dfrac {y''(0)}{{e}^{2}}+\dfrac {{(1-{e}^{3})}^{2}}{{e}^{2}}$。解得 $y''(0)={e}^{3}(3{e}^{3}-4)$。