题目
lim_(x arrow 1) (sin^2(x-1))/(x^2)-1
$\lim_{x \rightarrow 1} \frac{\sin^{2}(x-1)}{x^{2}-1}$
题目解答
答案
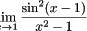 $\lim_{x \rightarrow 1} \frac{2\sin (x-1)cos(x-1)}{2x}$$=\lim_{x \rightarrow 1} \frac{2\sin (x-1) }{2x}$$=0$
$\lim_{x \rightarrow 1} \frac{2\sin (x-1)cos(x-1)}{2x}$$=\lim_{x \rightarrow 1} \frac{2\sin (x-1) }{2x}$$=0$
解析
考查要点:本题主要考查极限的计算方法,特别是处理0/0型不定式的能力,需要灵活运用洛必达法则或变量替换等技巧。
解题核心思路:
当直接代入$x=1$导致分母和分子均为0时,优先考虑洛必达法则。通过求分子和分母的导数,将原极限转化为新的分式极限。若仍为不定式,可重复应用洛必达法则或进一步化简。
破题关键点:
- 识别分母$x^2-1$可分解为$(x-1)(x+1)$,分子$\sin^2(x-1)$可视为$\sin(x-1) \cdot \sin(x-1)$。
- 应用洛必达法则后,分子导数为$2\sin(x-1)\cos(x-1)$,分母导数为$2x$,简化后直接代入$x=1$即可求得极限。
步骤1:验证极限类型
当$x \rightarrow 1$时,分子$\sin^2(x-1) \rightarrow 0$,分母$x^2-1 \rightarrow 0$,属于0/0型不定式,可应用洛必达法则。
步骤2:应用洛必达法则
对分子和分母分别求导:
- 分子导数:$\frac{d}{dx} \sin^2(x-1) = 2\sin(x-1)\cos(x-1)$
- 分母导数:$\frac{d}{dx} (x^2-1) = 2x$
原极限转化为:
$\lim_{x \rightarrow 1} \frac{2\sin(x-1)\cos(x-1)}{2x}$
步骤3:化简并代入极限
约分后得:
$\lim_{x \rightarrow 1} \frac{\sin(x-1)\cos(x-1)}{x}$
当$x \rightarrow 1$时,$\sin(x-1) \rightarrow 0$,$\cos(x-1) \rightarrow 1$,分母$x \rightarrow 1$,因此整体极限为:
$\frac{0 \cdot 1}{1} = 0$