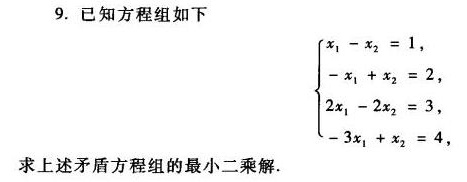
9.已知方程组如下-|||- ) (x)_(1)-(x)_(2)=1, -(x)_(1)+(x)_(2)=2, 2(x)_(1)-2(x)_(2)=3, -3(x)_(1)+(x)_(2)=4 .-|||-求上述矛盾方程组的最小二乘解.
题目解答
答案
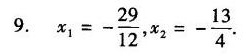
解析
考查要点:本题主要考查矛盾方程组的最小二乘解的求解方法,需要掌握正规方程的建立与求解。
解题核心思路:
当方程组无解时,最小二乘法通过最小化残差平方和找到最佳近似解。具体步骤为:
- 将方程组写成矩阵形式 $Ax = b$;
- 构造并解正规方程 $A^T A x = A^T b$;
- 得到最小二乘解 $x$。
破题关键点:
- 正确构建矩阵 $A$ 和向量 $b$;
- 准确计算 $A^T A$ 和 $A^T b$;
- 解二元一次方程组时注意行列式法或消元法的应用。
将方程组写成矩阵形式 $Ax = b$:
$A = \begin{bmatrix}1 & -1 \\-1 & 1 \\2 & -2 \\-3 & 1\end{bmatrix}, \quad
x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}, \quad
b = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}$
步骤1:计算 $A^T A$ 和 $A^T b$
$A^T A = \begin{bmatrix}1^2 + (-1)^2 + 2^2 + (-3)^2 & 1 \cdot (-1) + (-1) \cdot 1 + 2 \cdot (-2) + (-3) \cdot 1 \\(-1) \cdot 1 + 1 \cdot (-1) + (-2) \cdot 2 + 1 \cdot (-3) & (-1)^2 + 1^2 + (-2)^2 + 1^2\end{bmatrix} = \begin{bmatrix}15 & -9 \\-9 & 7\end{bmatrix}$
$A^T b = \begin{bmatrix}1 \cdot 1 + (-1) \cdot 2 + 2 \cdot 3 + (-3) \cdot 4 \\(-1) \cdot 1 + 1 \cdot 2 + (-2) \cdot 3 + 1 \cdot 4\end{bmatrix} = \begin{bmatrix}-7 \\-1\end{bmatrix}$
步骤2:解正规方程 $A^T A x = A^T b$
方程组为:
$\begin{cases}15x_1 - 9x_2 = -7 \\-9x_1 + 7x_2 = -1\end{cases}$
计算行列式 $D = 15 \cdot 7 - (-9) \cdot (-9) = 24$,代入克莱姆法则:
$x_1 = \frac{\begin{vmatrix} -7 & -9 \\ -1 & 7 \end{vmatrix}}{D} = \frac{-58}{24} = -\frac{29}{12}, \quad
x_2 = \frac{\begin{vmatrix} 15 & -7 \\ -9 & -1 \end{vmatrix}}{D} = \frac{-78}{24} = -\frac{13}{4}$