题目
(2)数列 √2, sqrt (2+sqrt {2)} , √(2+√2+√2),··· 的极限存在
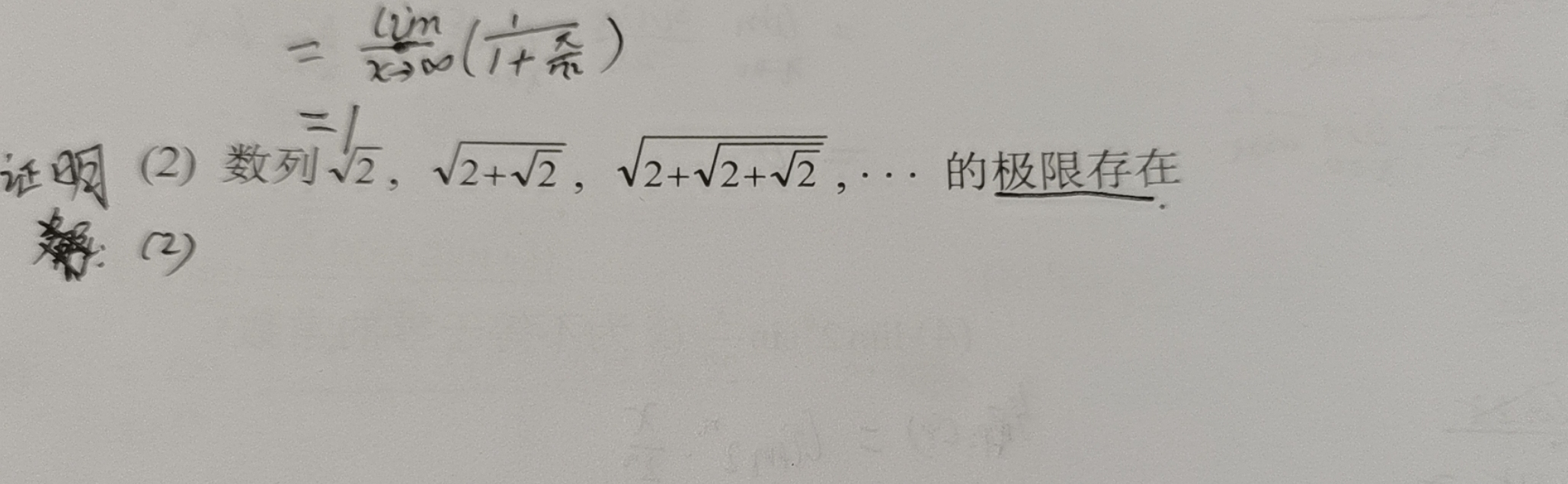
题目解答
答案

解析
考查要点:本题主要考查递归数列极限的存在性证明及求解方法,涉及单调有界定理的应用和递推关系求极限的技巧。
解题核心思路:
- 证明数列单调性:通过数学归纳法或直接比较相邻项,证明数列单调递增。
- 证明数列有界性:通过归纳法或不等式推导,证明数列存在上界。
- 利用极限定义求解:假设极限存在,代入递推关系式解方程求出极限值。
破题关键点:
- 单调性证明的关键在于通过递推关系式推导出$x_{n+1} > x_n$。
- 有界性证明需找到合适的上界(如$2$),并用归纳法验证。
- 极限方程的建立需注意平方操作后的解筛选,排除不符合实际的负根。
证明极限存在
步骤1:证明数列单调递增
- 基础情形:$x_1 = \sqrt{2} \approx 1.414$,$x_2 = \sqrt{2 + \sqrt{2}} \approx 1.847$,显然$x_2 > x_1$。
- 归纳假设:假设$x_{n} > x_{n-1}$成立。
- 递推关系:由$x_{n+1} = \sqrt{2 + x_n}$,若$x_n > x_{n-1}$,则$x_{n+1} = \sqrt{2 + x_n} > \sqrt{2 + x_{n-1}} = x_n$。
因此,数列$\{x_n\}$单调递增。
步骤2:证明数列有上界
- 基础情形:$x_1 = \sqrt{2} < 2$。
- 归纳假设:假设$x_n < 2$。
- 递推关系:$x_{n+1} = \sqrt{2 + x_n} < \sqrt{2 + 2} = \sqrt{4} = 2$。
因此,数列$\{x_n\}$有上界$2$。
结论:
由单调有界定理,数列$\{x_n\}$极限存在。
求极限值
设极限为$L$,则递推关系在极限下变为:
$L = \sqrt{2 + L}$
两边平方得:
$L^2 = 2 + L \quad \Rightarrow \quad L^2 - L - 2 = 0$
解得:
$L = \frac{1 \pm \sqrt{1 + 8}}{2} = \frac{1 \pm 3}{2} \quad \Rightarrow \quad L = 2 \text{ 或 } L = -1$
因数列各项均为正数,故$L = 2$。