题目
题目：[例6.12]设由线 =y(x)(ygt 0) 上任一点M(x,y)处的切线与x轴交于点N,且-|||-|OM|=|ON| (0)=1, '(x)gt 0, 求 =y(x).0)(上任一点)M(x,y)(处的切线与)x(轴交于点)N(,且) &|OM|=|ON|_(}^),y(0)=1,y^(prime(x)>0,{求 )y=y(x).. " data-width="652" data-height="91" data-size="17032" data-format="png" style="max-width:100%">
题目：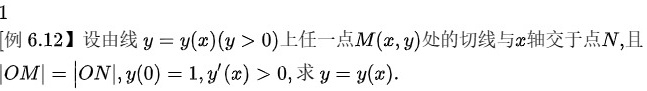
0)\text{上任一点}M(x,y)\text{处的切线与}x\text{轴交于点}N\text{,且} \\
&\left|OM\right|=\left|ON|_{}^{},y(0)=1,y^{\prime}(x)>0,\text{求 }y=y(x).\right.
\end{aligned}" data-width="652" data-height="91" data-size="17032" data-format="png" style="max-width:100%">
题目解答
答案
解答：
0\text{,所以导数存在,解得 }x=0\text{。} \\
&\text{代入初始条件 }y(0)=1\text{,得到 }y=\sqrt{x^2+y^2}=\sqrt{0^2+1^2}=1 \\
&\text{因此,所求的曲线方程为 }y=1。 \\
&\text{综上所述,解题过程如上所示,最终得到曲线方程 }y=1.
\end{aligned}" data-width="512" data-height="321" data-size="56539" data-format="png" style="max-width:100%">