设5个晶体管中有2个次品,3个正品,如果每次从中任取1个进行测试,测试后的产品不放回,直到把2个次品都找到为止,则需要进行的测试次数§是一个随机变量,则求Pl§Pl和Pl§Pl
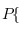 §
§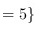 和
和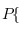 §
§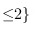
题目解答
答案
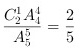
根据题意 §
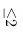 只存在§=2这一种情况,
只存在§=2这一种情况,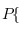 §
§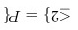 §
§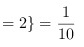
.
解析
本题考查古典概型的知识,解题思路是先确定随机变量的取值情况,再根据排列组合的公式公式计算相应的概率。
计算 $P\{\xi = 5\}$ 的计算
当 $\xi = 5$ 时,意味着最后一次取到的是次品。
从 $2$ 个次品中选 $1$ 个,有 $C_{2}^{1}$ 种选法;从 $4$ 个正品中选 $4$ 个进行全排列,有 $A_{4}^{4}$ 种法。
而从 $5$ 个产品中选 $5$ 个进行全排列,有 $A_{5}^{5}$ 种法。
根据古典概型概率公式 $P(A)=\frac{m}{n}$(其中 $m$ 是事件 $A$ 包含的基本事件个数,$n$ 是基本事件总数总数),可得 $P\{\xi = 5\frac{C_{2}^{1}A_{4}^{4}}{A_{5}^{5}}$。
计算 $C_{2}^{1}=\frac{2\}$,$A_{4}^{4}=4\times3\times2\times1 = 24$,$A_{5^{5}=5\times4\times3\times2\times1 = 120$,则 $\frac{C_{2}^{1}A_{4}^{4}}{A_{5}^{5}}=\frac{2\times24}{120}=\frac{2}{5}$。
$P\{\xi\leqslant 2\}$ 的计算
根据题意,$\xi\leqslant 2$ 只存在 $\xi = 2$ 这一种情况。
当 $\xi = 2$ 时,意味着前两次都取到次品。
从 $2$ 个次品中选 $2$ 个进行全排列,有 $A_{2}^{2}$ 种法;从 $3$ 个正品中选 $3$ 个进行全排列,有 $A_{3}^{3}$ 法。
从 $5$ 个产品中选 $5$ 个进行全排列,有 $A_{5}^{5}$ 法。
根据古典概型概率公式,可得 $P\{\xi = 2\}=\frac{A_{2}^{2}A_{3}^{3}}{A_{5}^{5}}$。
计算 $A_{2}^{2}=2\times1 = 2$,$A_{3^{3}=3\times2\times1 = 6$,$A_{5}^{5}=5\times4\times3\times2\times1 = 120$,则 $\frac{A_{2}^{2}A_{3}^{3}}{A_{5}^{5}}=\frac{2\times6}{120}=\frac{1}{10}$。
所以 $P\{\xi\leqslant 2\}==P\{\xi = 2\}=\frac{1}{10}$。