设随机变量X1,X 2独立同分布,其概率密度函数为-|||-f(x)= ) (e)^-x,xgt 0 0," data-width="617" data-height="120" data-size="19650" data-format="png" style="">
0\\0,\text{其它}\end{cases},\\&\text{令}Y_1=\min\left\{X_1,X_2\right\},Y_2=\max\left\{X_1,X_2\right\},\text{ 求}\left(Y_1,Y_2\right)\text{的联合分布函数}.\end{aligned}" data-width="617" data-height="120" data-size="19650" data-format="png" style="">
题目解答
答案
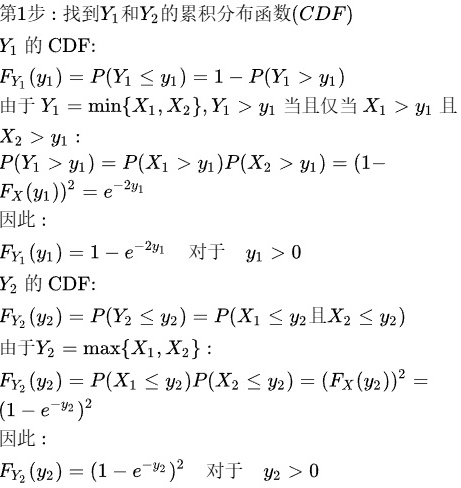y_{1}) \\ &\text{由于 }Y_1=\min\{X_1,X_2\},Y_1>y_1\text{ 当且仅当 }X_1>y_1\text{ 且} \\ &X_{2}>y_{1}: \\ &P(Y_1>y_1)=P(X_1>y_1)P(X_2>y_1)=(1- \\ &F_X(y_1))^2=e^{-2y_1} \\ &因此: \\ &F_{Y_{1}}(y_{1})=1-e^{-2y_{1}}\quad\text{对于}\quad y_{1}>0 \\ &Y_{2}\text{ 的 CDF:} \\ &F_{Y_{2}}(y_{2})=P(Y_{2}\leq y_{2})=P(X_{1}\leq y_{2} \text{且} X_{2}\leq y_{2}) \\ &\text{由于}Y_{2}=\max\{X_{1},X_{2}\}: \\ &F_{Y_2}(y_2)=P(X_1\leq y_2)P(X_2\leq y_2)=(F_X(y_2))^2= \\ &(1-e^{-y_2})^2 \\ &因此: \\ &F_{Y_{2}}(y_{2})=(1-e^{-y_{2}})^{2}\quad\text{对于}\quad y_{2}>0 \end{aligned}" data-width="466" data-height="488" data-size="49309" data-format="png" style="">
y_{2}: \\ &F_{Y_{1},Y_{2}}(y_{1},y_{2})=0 \\ &因此,联合分布函数是: \\ &F_{Y_1,Y_2}(y_1,y_2)=\begin{cases}0,&\text{如果 }y_1>y_2\$1-e^{-y_2})^2,&\text{如果 }0
解析
- Y1的CDF: ${F}_{1}({y}_{1})=P({Y}_{1}\leqslant {y}_{1})=1-P({Y}_{1}\gt {y}_{1})$
- 由于 ${Y}_{1}=min\{ {X}_{1},{X}_{2}\} $ ${Y}_{1}\gt {y}_{1}$ 当且仅当 ${X}_{1}\gt {y}_{1}$ 且 X2>y1:
- P(Y1>y1)=P(X 1>y1)P(X2 >y1)=(1- Fx(y1))^2=e^(-2y1)
- 因此: ${F}_{{Y}_{1}}({y}_{1})=1-{e}^{-2{y}_{1}}$ 对于 ${y}_{1}\gt 0$
- Y2的CDF: ${F}_{{Y}_{2}}({y}_{2})=P({Y}_{2}\leqslant {y}_{2})=P({X}_{1}\leqslant {y}_{2}且{X}_{2}\leqslant {y}_{2})$
- 由于 ${Y}_{2}=max\{ {X}_{1},{X}_{2}\} $ : ${F}_{{l}_{2}}({y}_{2})=P({x}_{1}\leqslant {y}_{2})P({x}_{2}\leqslant {y}_{2})={({F}_{x}{({y}_{2})}^{2}=$ ${(1-{e}^{-{y}_{2}})}^{2}$
- 因此: ${F}_{{Y}_{2}}({y}_{2})={(1-{e}^{-{y}_{2}})}^{2}$ .对于 ${y}_{2}\gt 0$
步骤 2：找到(Y11,Y2)的联合分布函数
- 联合分布函数FY1 ,22(y1,y2)由下式给出: ${F}_{{1}_{1}}{x}_{2}({y}_{1},{y}_{2})=P({Y}_{1}\leqslant {y}_{1}且{Y}_{2}\leqslant {y}_{2})$
- 对于 ${y}_{1}\leqslant {y}_{2}$ : ${F}_{{y}_{2}}({y}_{2})=P({x}_{1}\leqslant {y}_{2}且{x}_{2}\leqslant {y}_{2})={(1-{e}^{-{y}_{2}})}^{2}$
- 对于 ${y}_{1}\gt {y}_{2}$ : ${F}_{{Y}_{1}{Y}_{2}}({y}_{1},{y}_{2})=0$
- 因此,联合分布函数是: ${F}_{{Y}_{1}}{Y}_{2}({y}_{1},{y}_{2})=$ $\left \{ \begin{matrix} 0,\\ {(1-{e}^{-{y}_{2}})}^{2}\end{matrix} \right.$ 如果 $0\lt {y}_{1}\leqslant {y}_{2}$ 如果 ${y}_{1}\gt {y}_{2}$